Een driehoek is een meetkundige figuur die ontstaat door drie punten die niet op een rechte lijn liggen met elkaar te verbinden. De verbindende lijnstukken heten de zijden van de driehoek. De driehoek met de hoekpunten A,B en C wordt genoteerd als \triangle ABC. Meestal worden voor een willekeurige driehoek de hoekpunten zo gekozen als in de figuur: links het hoekpunt A, rechts B en in de top C. De hoeken van de driehoek worden meestal overeenkomstig de hoekpunten aangeduid met α, β en γ, en de zijden van de driehoek met de letters a, b en c, zodat a de tegenover A liggende zijde is, b tegenover B ligt en c tegenover C.
Een driehoek is een 2-simplex.
Pythagoras bewees dat de som van de hoeken van een driehoek steeds 180 graden is, al denkt men dat de ontdekking gedaan werd door een leerling van hem en uit respect aan hem werd toegeschreven.
\alpha + \beta + \gamma = 180^o (https://nl.wikipedia.org/wiki/Driehoek_(meetkunde))
Een simplex of n-simplex is een n-dimensionaal analogon van de driehoek. Preciezer is het het convexe omhulsel van n+1 onafhankelijke punten, dat wil zeggen dat geen m+2 van de punten in een m-dimensionale deelruimte liggen (https://nl.wikipedia.org/wiki/Simplex_(wiskunde)).
Er bestaan verschillende driehoeken:
Er zijn verschillende soorten driehoeken.
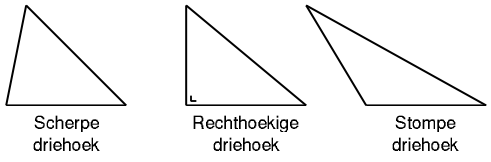
Indeling op basis van de hoeken:
scherpe driehoek: alle hoeken zijn kleiner dan 90 graden.
rechthoekige driehoek: een van de hoeken is 90 graden.
stompe driehoek: een van de hoeken is groter dan 90 graden.
Indeling op basis van de zijden:
gelijkbenige driehoek: er zijn twee of drie even lange zijden. In het laatste geval is de driehoek gelijkzijdig (elke gelijkzijdige driehoek is ook gelijkbenig). De beide hoeken die aan de derde zijde grenzen( de basishoeken)zijn aan elkaar gelijk.
gelijkzijdige driehoek: alle zijden zijn even lang. De drie hoeken zijn ook even groot, namelijk 60°. Verder is vanuit ieder hoekpunt de zwaartelijn tevens de bissectrice en de hoogtelijn. Daarnaast ontstaat er door zes gelijkzijdige driehoeken in elkaar te schuiven een regelmatige zeshoek. Een gelijkzijdige driehoek is een voorbeeld van een regelmatige veelhoek. De formule voor de oppervlakte O van een gelijkzijdige driehoek met zijden van z cm is (https://nl.wikipedia.org/wiki/Driehoek_(meetkunde))
Als de drie hoekpunten op één lijn liggen, is er geen sprake van een echte driehoek. Een van de hoeken is dan 180 graden, de andere twee hoeken zijn 0 graden. Omdat het toch zinvol kan zijn over zo'n driehoek te spreken, wordt die driehoek ontaard genoemd (https://nl.wikipedia.org/wiki/Driehoek_(meetkunde))
In de voedselwetenschap wordt doorgaans de ‘Triangle Test’ gebruikt om te kijken of er een waarneembaar verschil bestaat tussen twee producten. Dat gaat zo:
De proefpersoon proeft (blind) drie drankjes: twee dezelfde en één afwijkende. In dit geval gaan we voor twee Schultenbräu's (Op YouTube staat Schultenbräu bekend als het biermerk met 'de slechtste commercial ooit.' en één Heineken.) Na het proeven probeert de speler de afwijkende pilsener eruit te pikken. Haal je het Heinekenpilsje er significant vaker uit dan in één derde van de gevallen, dan doe je het beter dan een chimpansee (https://decorrespondent.nl/2657/De-Grote-Correspondent-Pils-Test/102148365-b2c234db). Ik heb wel eens Sanne Hans van Miss Montreal op 3FM pils horen proeven, ze had er volgens mij Amstel, Bavaria, Heineken en Grolsch en die haalde ze er goed uit! Het is dus wel te doen! Of het was vooropgezet scripted reality...
Een driehoek is een 2-simplex.
Pythagoras bewees dat de som van de hoeken van een driehoek steeds 180 graden is, al denkt men dat de ontdekking gedaan werd door een leerling van hem en uit respect aan hem werd toegeschreven.
\alpha + \beta + \gamma = 180^o (https://nl.wikipedia.org/wiki/Driehoek_(meetkunde))
Een simplex of n-simplex is een n-dimensionaal analogon van de driehoek. Preciezer is het het convexe omhulsel van n+1 onafhankelijke punten, dat wil zeggen dat geen m+2 van de punten in een m-dimensionale deelruimte liggen (https://nl.wikipedia.org/wiki/Simplex_(wiskunde)).
Er bestaan verschillende driehoeken:
Er zijn verschillende soorten driehoeken.
Indeling op basis van de hoeken:
scherpe driehoek: alle hoeken zijn kleiner dan 90 graden.
rechthoekige driehoek: een van de hoeken is 90 graden.
stompe driehoek: een van de hoeken is groter dan 90 graden.
Indeling op basis van de zijden:
gelijkbenige driehoek: er zijn twee of drie even lange zijden. In het laatste geval is de driehoek gelijkzijdig (elke gelijkzijdige driehoek is ook gelijkbenig). De beide hoeken die aan de derde zijde grenzen( de basishoeken)zijn aan elkaar gelijk.
gelijkzijdige driehoek: alle zijden zijn even lang. De drie hoeken zijn ook even groot, namelijk 60°. Verder is vanuit ieder hoekpunt de zwaartelijn tevens de bissectrice en de hoogtelijn. Daarnaast ontstaat er door zes gelijkzijdige driehoeken in elkaar te schuiven een regelmatige zeshoek. Een gelijkzijdige driehoek is een voorbeeld van een regelmatige veelhoek. De formule voor de oppervlakte O van een gelijkzijdige driehoek met zijden van z cm is (https://nl.wikipedia.org/wiki/Driehoek_(meetkunde))
Met een formule kun je bijvoorbeeld de oppervlakte uitrekenen.
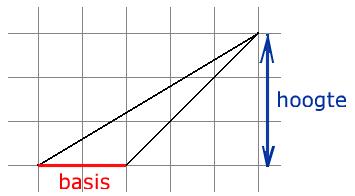
Voor een driehoek geldt de formule: oppervlakte = 1/2 x basis x hoogte
Wat de 'basis' en wat de 'hoogte' is, kun je in de figuur zien (http://leestrainer.nl/Leerlijn%20Rekenen/groep/cijferen/driehoek.htm). De formules om de oppervlakte van een driehoek te berekenen zijn:
1/2×Basis×Hoogte
en
√(Omtrek×(Omtrek-Zijde 1)×(Omtrek-Zijde 2)×(Omtrek-Zijde 3))
De basis is de korte zijde van de driehoek. De hoogte is de kortste afstand van die zijde tot het tegenoverliggende punt. Hierbij geldt dat de hoogte en de basis altijd loodrecht op elkaar staan (www.berekenen.nl/a-z/oppervlakte-driehoek-berekenen).
De stelling van Pythagoras is een wiskundige stelling die haar naam dankt aan de Griekse wiskundige Pythagoras. 'Zijn' stelling was overigens alleen maar nieuw voor de Grieken. In Soemerië was het resultaat al veel langer bekend, en ook in Babylonië en het oude Egypte werd ze al eerder toegepast (met name de verhouding a=3;b=4;c=5 werd al vroeg gebruikt om rechte hoeken uit te meten, zoals dat tot op de dag van vandaag door sommigen nog wordt gedaan). Echter, belangrijker dan de kennis van de stelling om haar enkel toe te passen, is het leveren van een bewijs. Wat dat betreft waren de Grieken (Pythagoras of een van zijn leerlingen) wel de eersten. Zij wisten niet alleen dat de stelling waar was, maar konden ook in algemene termen (abstracties) aantonen waarom zij waar was (https://nl.wikipedia.org/wiki/Stelling_van_Pythagoras).
De stelling van Pythagoras geeft een verband tussen de lengten van de zijden van een rechthoekige driehoek. In woorden luidt de stelling:
In een rechthoekige driehoek is de som van de kwadraten van de lengtes van de rechthoekszijden gelijk aan het kwadraat van de lengte van de schuine zijde.
Noemen we de lengten van rechthoekszijden (de zijden die aan de hoek van 90° liggen) a en b, en de lengte van de schuine zijde (de zijde die niet aan de rechte hoek grenst, ook wel "hypotenusa" genoemd) c, dan is de bekende wiskundige vorm van de stelling:
\!a^2 + b^2 = c^2
(Dit is Propositie I.47 uit de Elementen van Euclides)
De stelling van Pythagoras is equivalent met het parallellenpostulaat. Daarom geldt de stelling van Pythagoras niet in niet-euclidische meetkunde (https://nl.wikipedia.org/wiki/Stelling_van_Pythagoras).
Ik heb al eens eerder over driehoeken geschreven, De Belg Jean-François Van Boxmeer durft blijkbaar wel wat Karel Vuursteen niet durfde.
In de voedselwetenschap wordt doorgaans de ‘Triangle Test’ gebruikt om te kijken of er een waarneembaar verschil bestaat tussen twee producten. Dat gaat zo:
De proefpersoon proeft (blind) drie drankjes: twee dezelfde en één afwijkende. In dit geval gaan we voor twee Schultenbräu's (Op YouTube staat Schultenbräu bekend als het biermerk met 'de slechtste commercial ooit.' en één Heineken.) Na het proeven probeert de speler de afwijkende pilsener eruit te pikken. Haal je het Heinekenpilsje er significant vaker uit dan in één derde van de gevallen, dan doe je het beter dan een chimpansee (https://decorrespondent.nl/2657/De-Grote-Correspondent-Pils-Test/102148365-b2c234db). Ik heb wel eens Sanne Hans van Miss Montreal op 3FM pils horen proeven, ze had er volgens mij Amstel, Bavaria, Heineken en Grolsch en die haalde ze er goed uit! Het is dus wel te doen! Of het was vooropgezet scripted reality...
.svg/260px-Bermuda_Triangle_(NL).svg.png)